как вычислить отрицательное ускорение?

acceleration = (force / mass) 
velocity = (acceleration * time)
(force from user's finger) = acceleration / mass = velocity / time

1. придайте массе виду (настройте его до тех пор, пока все не покажется разумным, и позвольте пользователю настройте его)
2. определите некоторую новую силу (перетаскивание)
3. придайте новой силе (перетаскивание) величину (настройте до разумной степени, позвольте пользователю настроить ее)
4. примените новую силу к объекту и наблюдайте, как она замедляется вниз

[Краткий ответ (при условии синтаксиса C )]

double v(double old_v, double dt) {
    t = t_for(old_v); 
    new_t = t - dt; 
    return (new_t <= 0)?0:v_for(t);
} 

double t_for (double v) и double v_for (double t) являются возвращаемыми значениями из двунаправленное отображение v-to-t (функция в математическом смысле), которое является произвольным с ограничением, что оно является монотонным и определено для v> = 0 (и, следовательно, имеет точку, где v = 0 ). Пример:

double v_for(double t) { return pow(t, k); }
double t_for(double v) { return pow(v, 1.0/k); }

где наличие:

1. k> 1 дает замедление, уменьшающееся по модулю с течением времени.
2. k <1 дает замедление, увеличивающееся по модулю с течением времени.
3. k = 1 дает постоянное замедление.

[Более длинный (с обоснованием и сюжетами)]

Итак, основная цель:

1. Чтобы найти функцию v (t + dt) = f (v (t), dt) , которая принимает текущее значение скорости v и временную дельту dt и возвращает скорость в настоящий момент t + dt (это не требует фактического указания t , поскольку v (t) уже известно и предоставляется как параметр, а ] dt - это просто дельта времени). Другими словами, задача состоит в том, чтобы реализовать подпрограмму double next_v (curr_v, dt); со специфическими свойствами (см. Ниже).

2. [Обратите внимание] У рассматриваемой функции есть полезный (и желательный) свойство возвращать один и тот же результат независимо от "истории" предыдущих изменений скорости.Это означает, что, например, если серия последовательных скоростей равна [100, 50, 10, 0] (для начальной скорости v0 = 100 ), любая другая последовательность, превышающая эту, будет иметь такую ​​же "хвост": [150, 100, 50, 10, 0] (для начальной скорости v0 = 150 ) и т. д. Другими словами, независимо от начальной скорости, все скорости -временные графики будут фактически копиями друг друга, просто смещенными вдоль оси времени каждый на свое собственное значение (см. график ниже, обратите внимание на части графиков между линиями t = 0.0 и t = 2.0 идентичны) .

3. Кроме того, ускорение w (t) = dv (t) / dt должно быть убывающей функцией времени t (для визуально приятного и «интуитивного» поведения движущийся объект GUI, который мы здесь моделируем).

Предлагаемая идея такова:

1. Сначала вы выбираете монотонную функцию скорости с желаемыми свойствами (в вашем случае ускорение постепенно уменьшается, хотя, как показано в примере ниже, ее проще использовать «ускоренные»). Эта функция также не должна иметь верхней границы , чтобы вы могли использовать ее для любых больших значений скорости. Кроме того, он должен иметь точку, в которой скорость равна нулю . Вот несколько примеров: v (t) = k * t (не совсем ваш случай, поскольку замедление k здесь постоянно), v = sqrt (-t) (это нормально, определяется на интервале t <= 0 ).

2. Затем для любой заданной скорости вы найдете точку с этим значением скорости на приведенном выше графике функции (будет точка, поскольку функция не привязана, и только одна, поскольку она монотонная), продвигаясь по временной дельте. к меньшим значениям скорости, таким образом приобретая следующий. Итерация постепенно (и неизбежно) приведет вас к точке, где скорость равна нулю.

3. Вот и все, нет даже необходимости создавать какую-то «окончательную» формулу, зависимости от значения времени или начальной (не текущей) скорости исчезают, и программирование становится действительно простым .

Для двух простых случаев этот небольшой скрипт Python создает графики ниже (начальные скорости были от 1.0 до 10.0 ), и, как вы можете видеть, из любого заданного «уровень» скорости и «вниз» графики «ведут себя» одинаково , что является причиной, потому что независимо от того, с какой скоростью вы начинаете замедляться (замедляться), вы «движетесь» по одной и той же кривой. до точки, в которой скорость (становится) нулевой :

import numpy
import pylab

import math


class VelocityCurve(object):
    """
    An interface for the velocity 'curve'.
    Must represent a _monotonically_ _growing_
        (i.e. with one-to-one correspondence
        between argument and value) function
        (think of a deceleration reverse-played)
    Must be defined for all larger-than-zero 'v' and 't'
    """
    def v(self, t):
        raise NotImplementedError

    def t(self, v):
        raise NotImplementedError



class VelocityValues(object):

    def __init__(self, v0, velocity_curve):
        assert v0 >= 0
        assert velocity_curve

        self._v = v0
        self._vc = velocity_curve

    def next_v(self, dt):
        t = self._vc.t(self._v)
        new_t = t - dt

        if new_t <= 0:
            self._v = 0
        else:
            self._v = self._vc.v(new_t)

        return self._v


class LinearVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=k*t'"""
        super(LinearVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return self._k*t

    def t(self, v):
        assert v >= 0
        return v/self._k


class RootVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=t^(1/k)'"""
        super(RootVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return math.pow(t, 1.0/self._k)

    def t(self, v):
        assert v >= 0
        return math.pow(v, self._k)


def plot_v_arr(v0, velocity_curve, dt):
    vel = VelocityValues(v0, velocity_curve)
    v_list = [v0]

    while True:
        v = vel.next_v(dt)
        v_list.append(v)

        if v <= 0:
            break

    v_arr = numpy.array(list(v_list))
    t_arr = numpy.array(xrange(len(v_list)))*dt

    pylab.plot(t_arr, v_arr)


dt = 0.1

for v0 in range(1, 11):
    plot_v_arr(v0, LinearVelocityCurve(1), dt)

for v0 in range(1, 11):
    plot_v_arr(v0, RootVelocityCurve(2), dt)


pylab.xlabel('Time ')
pylab.ylabel('Velocity')

pylab.grid(True)

pylab.show()

Это дает следующие графики (линейные для линейного замедления (т. е. постоянного замедления), "кривые" - для случая "квадратного корня") (см. код выше)):

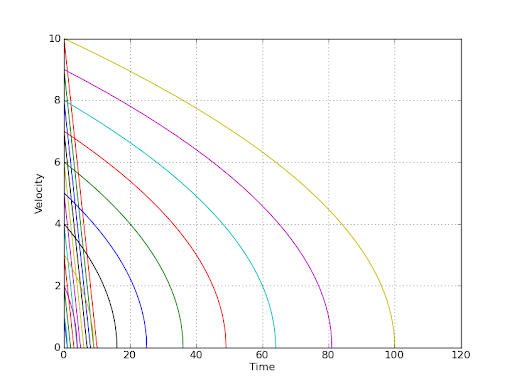
Также имейте в виду, что для запуска вышеуказанного скрипта необходимо установить pylab, numpy и друзья (но только для части построения графика, "основные" классы ни от чего не зависят и, конечно, можно использовать самостоятельно).

P.S.При таком подходе действительно можно «построить» (например, дополнить разные функции для разных t интервалов или даже сгладить нарисованную от руки (записанную) «эргономичную» кривую) понравившееся «перетаскивание» :)

Небольшое обсуждение примера автомобиля, не связанного с программированием.

Во-первых, я предполагаю, что водитель не может заставить тормоза заблокироваться на скорости.

Первое (а может быть, второе или третье) большинство начинающих водителей усваивают, что естественная тенденция при торможении - удерживать педаль тормоза в фиксированном положении. Результатом является внезапный крен вперед, когда машина переходит от медленного движения к остановке. Это происходит из-за того, что тормоза переходят от динамического трения, где тормозная сила пропорциональна тормозному давлению, к статическому трению, когда тормозная сила восстанавливает поступательный импульс автомобиля. этот внезапный скачок ускорения неприятен, и новый водитель учится нажимать на педаль в самом конце замедления, чтобы остановиться.

Такое поведение маскирует еще одну особенность, но это можно заметить при нормальном ускорении в автомобиле с механической коробкой передач. при ускорении (или замедлении), если водитель внезапно выключает передачу, все пассажиры внезапно кренится вперед. На самом деле происходит то, что ускоряющая сила, прижимавшая их к спинкам сидений, внезапно исчезает, и они возвращаются в нейтральное положение сидя. Более комфортный способ вождения - постепенно выжимать сцепление, чтобы движущая сила двигателя постепенно снижалась.

В обоих случаях более эстетичный стиль вождения предполагает сглаживание ускорений и устранение резких скачков. По сути, это еще один способ говорить о непрерывной второй производной. Практически любое движение с этим свойством будет казаться естественным.

Ускорение - это производная первого порядка от скорости и производная второго порядка от расстояния. Ваш график выглядит как парабола второго порядка, что-то вроде C-k * x ^ 2 для некоторых констант C и k. Если y действительно расстояние, вам нужно a = -2k, если y - скорость, вам нужно a = -2kx. В любом случае скорость v (x) = V0 + a (x) * x. (Где x на самом деле время. Я следую вашему соглашению и не использую t.)

Вы можете отслеживать скорость и каждый раз уменьшать ее на долю скорости. Я считаю, что это достаточно хорошо имитирует трение.

Я бы сократил скорость как что-то вроде v=v*0.9. Тогда у меня будет скорость, которая считается скоростью остановки. Таким образом, объект в конце концов придет в состояние покоя и не будет продолжать потреблять ресурсы при движении. Таким образом, что-то вроде for(v=startingVelocity;v<1.0;v*=0.9) { x+=v; }

Добавлю еще одну мысль. Похоже, что вы не хотите постоянного (отрицательного) ускорения. Это привело бы к уравнению типа:

v(t) = v(0) + a*t,

где a - отрицательное ускорение, t - время, и v(t) - скорость в момент времени t. Это дает:

v(t2) - v(t1) = a(t2-t1),

и означает, что для данного Δt разность скоростей равна aΔt, константе.

Возможно, вы ищете член "трения", который зависит от текущей скорости. При таком предположении скорость изменения скорости пропорциональна текущей скорости:

d v(t) / d t = -b*v(t).

Решить вышеприведенное уравнение легко, и вы получите: v(t) = v(0) e^{-b t}.

Интегрируя это уравнение, получаем x(t) = v(0)(1-e^{-b t}) / b, где x - положение. График положения¹ для v(0) = 1, b = 0.1 похож на то, что вы могли бы использовать. Играя со значениями b и добавляя масштабный коэффициент к уравнению, возможно, вы хотите сделать то, что нужно.

¹ http://www.wolframalpha.com/input/?i=plot+%281+-+1+e^%28-0.1+x%29+%29+%2F+0.1+for+x+%3D+0+to+100

Если вы хотите увеличить замедление, как вы говорите в своем комментарии к ответу mtrw, и вы НЕ очень разборчивы в отношении физического реализма, приведенное ниже уравнение может быть тем, что вы ищем:

V (t + dt) = V (t) - K1 + K2 x V (t)

V (t) = текущая скорость V (t + dt)= скорость при следующем приращении времени K1 и K2 - константы, которые вы калибруете. Просто убедитесь, что (K2 x Vmax)

Если это все еще кажется неправильным, попробуйте V (t + dt) = V (t) - K1 + K2 xf (V (t))

где f (x) - это монотонно возрастающая функция, которую вы выбираете, может быть квадратный или квадратный корень, в зависимости от того, где вы хотите передать ощущение. Просто убедитесь, что (K2 x f (V (t)))

(монотонно возрастающая функция означает, что f (x) всегда увеличивается при увеличении x)

Вы можете просто уменьшать скорость на постоянную величину каждую итерацию. Пример: вы начинаете со скоростью 50, на следующей итерации она становится 40, затем 30, 20, 10, стоп. Это будет представлять собой постоянное "трение", не зависящее от скорости, и это на самом деле довольно близко к реальности (см. трение в Википедии).

Если вам не нравится такой вид, вам нужно сделать трение зависимым от скорости. Я бы предположил, что линейной зависимости friction = base-friction + (коэффициент * скорость), с довольно маленьким коэффициентом, будет достаточно.

Пока машина замедляется, я хочу иметь возможность рассчитать скорость, которую она будет иметь ровно через секунду, исключительно на основе текущей скорости.

Это было бы определение ускорения. Например, если ускорение было a = -9 метров / сек / сек , а скорость сейчас составляет 20 метров / сек , то через 1 секунду скорость будет 11 метров / сек .

Другими словами, изменение скорости Δv между настоящим моментом и t секунд с этого момента (при условии постоянного ускорения) будет

Δv = a * t

, что означает, что уравнение (классической физики) для скорости в любое время t , учитывая начальную скорость в t = 0 (эта скорость называется v ₀ ) равно

v (t) = v ₀ + a * t

Используя то, что вы узнаете за первые две недели занятий по математике, вы также можете получить уравнение для x (t) (расстояние до автомобиля в момент времени t ) из приведенного выше уравнения; это даст вам

x (t) = x ₀ + v ₀ * t + 0,5 * a * t ²

(также возможно получить это без исчисления, см. здесь )

Наконец , если вы делаете это для игры, а не для моделирования физики (что означает, что вам не нужны точно точные результаты), вы получите хотите просто изменять положение и скорость каждый кадр, а не пересчитывать положение каждый кадр. Для этого вам нужно будет делать следующее каждый кадр, предполагая, что скорость (и ускорение) измеряется в пикселях в секунду (-в секунду):

velocity_new = velocity_old + acceleration/frames_per_second
position_new = position_old + velocity_old/frames_per_second

Прочитав комментарии, я хотел бы изменить свой ответ: Умножьте скорость на k <1, например k = 0,955, чтобы заставить его распадаться по экспоненте.

Объяснение (с графиками и настраиваемым уравнением!) следует ...

Я интерпретирую график в вашем исходном вопросе как показывающий, что скорость остается около начального значения, а затем все более быстро уменьшается. Но если вы представите, как скользите по столу книгой, она быстро удаляется от вас, затем замедляется, а затем останавливается. Я согласен с @Chris Farmer в том, что правильная модель для использования - это сила сопротивления, пропорциональная скорости.Я собираюсь взять эту модель и получить ответ, который я предложил выше. Я заранее извиняюсь за длину этого. Я уверен, что кто-нибудь, кто лучше разбирается в математике, может это значительно упростить. Кроме того, я помещаю ссылки на графики напрямую, в ссылках есть некоторые символы, которые не нравятся синтаксическому анализатору SO. Исправлены URL-адреса.

Я собираюсь использовать следующие определения:

x -> time
a(x) -> acceleration as a function of time
v(x) -> velocity as a function of time
y(x) -> position as a function of time
u -> constant coefficient of drag
colon : denotes proportionality

Мы знаем, что сила сопротивления пропорциональна скорости. Мы также знаем, что сила пропорциональна ускорению.

a(x) : -u v(x)        (Eqn. 1)

Знак минус означает, что ускорение противоположно текущему направлению движения.

Мы знаем, что скорость - это интегрированное ускорение.

v(x) : integral( -u v(x) dx )        (Eqn. 2)

Это означает, что скорость пропорциональна собственному интегралу. Мы знаем, что e ^ x удовлетворяет этому условию. Итак, мы предполагаем, что

v(x) : e^(-u x)        (Eqn. 3)

Коэффициент сопротивления в показателе экспоненты таков, что когда мы решаем интеграл в уравнении. 2 u отменяется, чтобы вернуться к уравнению. 3.

Теперь нам нужно вычислить значение u . Как указал @BlueRaja , e ^ x никогда не равно нулю, независимо от x. Но он стремится к нулю при достаточно отрицательном x. Предположим, что 1% нашей исходной скорости «остановлен» (ваше представление о пороге) , и предположим, что мы хотим остановиться в течение x = 2 секунд (вы можете настроить это позже). Затем нам нужно решить

e^(-2u) = 0.01        (Eqn. 4)

, что приводит нас к вычислению

u = -ln(0.01)/2 ~= 2.3        (Eqn. 5)

Давайте граф v (x) .

Похоже, он экспоненциально спадает до небольшого значения за 2 секунды. Все идет нормально.

Мы не обязательно хотим вычислять экспоненты в нашем графическом интерфейсе. Мы знаем, что можем легко преобразовать экспоненциальное основание,

e^(-u x) = (e^-u)^x        (Eqn. 6)

Мы также не хотим отслеживать время в секундах. Мы знаем, что у нас частота обновления 20 мс, поэтому давайте определим метку n со скоростью 50 тиков в секунду.

n = 50 x        (Eqn. 7)

Подставляя значение u из уравнения. 5 в уравнение. 6, в сочетании с уравнением. 7, и подставив в уравнение. 3, мы получаем

v(n) : k^n, k = e^(ln(0.01)/2/50) ~= 0.955        (Eqn. 8)

Давайте начертим это с нашей новой осью x в метках времени.

Опять же, наша функция скорости пропорциональна чему-то, что убывает до 1% за желаемое количество итераций и следует модели «выбега под действием трения». Теперь мы можем умножить нашу начальную скорость v0 на уравнение. 8, чтобы получить фактическую скорость на любом временном шаге n:

v(n) = v0 k^n        (Eqn. 9)

Обратите внимание, что в реализации нет необходимости отслеживать v0! Мы можем преобразовать замкнутую форму v0 * k ^ n в рекурсию, чтобы получить окончательный ответ

v(n+1) = v(n)*k        (Eqn. 10)

. Этот ответ удовлетворяет вашему ограничению не заботиться о начальной скорости - следующая скорость всегда может рассчитываться с использованием только текущей скорости.

Стоит проверить, имеет ли смысл поведение позиции. Положение после такой модели скорости

y(n) = y0 + sum(0..n)(v(n))        (Eqn. 11)

Сумма в уравнении. 11 легко решается с использованием формы уравнения 9 . Используя индексную переменную p:

sum(p = 0..n-1)(v0 k^p) = v0 (1-k^n)/(1-k)        (Eqn. 12)

Итак, у нас есть

y(n) = y0 + v0 (1-k^n)/(1-k)        (Eqn. 13)

. Построим это как y0 = 0 и v0 = 1 .

Итак, мы видим быстрое движение от начала, следуя по изящному берегу до остановки.Я считаю, что этот график является более точным изображением скольжения, чем ваш исходный график.

В общем, вы можете настроить k с помощью уравнения

k = e^(ln(Threshold)/Time/Tickrate)        (Eqn. 14)
where:
Threshold is the fraction of starting velocity at which static friction kicks in
Time is the time in seconds at which the speed should drop to Threshold
Tickrate is your discrete sampling interval

(СПАСИБО @poke за демонстрацию использования Wolfram Alpha для построения графиков - это довольно мило).

СТАРЫЙ ОТВЕТ

Умножьте скорость на k <1, например, k = 0,98, чтобы заставить ее убывать экспоненциально.

y(x) = y0 - a * e ^ ( k * x )

где y0 - начальная константа, а a и k - множители.

Пример сюжета .

Я попробовал это, и это работает (в Ruby). Не уверен, что математика верна, но вывод выглядит правильно, то есть вы становитесь быстрее по мере приближения к центру:

velocity=100;
(100.downto(0)).each { |distance_from_black_hole |  velocity=velocity+9.8/distance_from_black_hole; puts velocity; }

Похоже, вы ищете замедление, которое со временем увеличивается.

Попробуйте вычислить

Delta_v = - (A * t + B) , выбрав разумные константы A и B, которые вам подходят.

t - полное время до этого момента.

Измените скорость, добавив Delta_v .

Это в основном соответствует линейному отрицательному ускорению.

В принципе, вы можете выбрать любую функцию, которая увеличивается со временем (скажем, f (t))

и вычислить

Delta_v = -f(t)

. Подходящий выбор для f (t) даст вам желаемый эффект.

Некоторые примеры, которые вы можете использовать:

f(t) = At + B.
f(t) = A*exp(Bt)

Конечно, вам придется немного поэкспериментировать и попытаться вычислить правильные константы.

Нелинейное изменение скорости означает, что ускорение не является постоянным. Непостоянное ускорение означает, что система находится под влиянием рывка . Возьмите все свои уравнения ускорения и добавьте «(1/6) jt ³ ». Исправьте a и присвойте j небольшое отрицательное значение, пока v не достигнет 0.